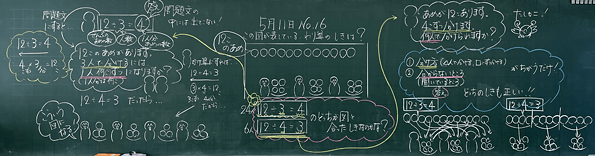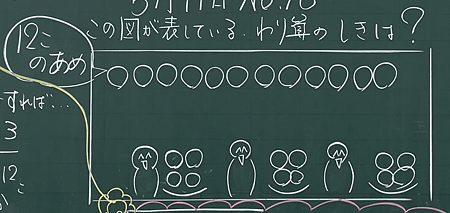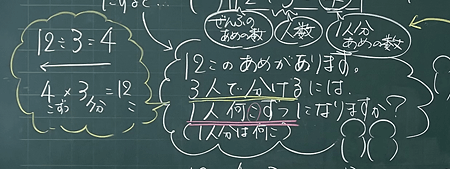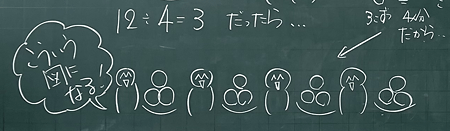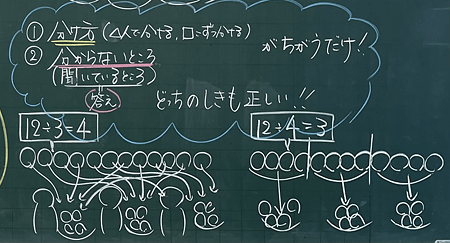- とっておき算数授業
- 算数・数学
本時のねらい
わり算には等分除と包含除があることを理解し、図や問題文からその違いを区別することができる。
板書
板書のとっておきポイント
- 大きく黒板を3分割している。(左:12÷3=4に関する話題、中央:図と中心課題、右:12÷4=3に関する話題とまとめ)
- 話合いのメインとなる図と中心課題を黒板の中心に据え、黒板の左右で考えを比較しやすくした。
授業の流れ
1図から式を想像させ、考えのずれから問いをもつ(10分)
問題文を提示する。
この図が表しているわり算の式は何でしょうか?
上の写真の図を提示する。今回は図をかいているとき、子どもたちは目を閉じさせ、かいている順序が分からないようにした。画用紙などにあらかじめかいたものを提示するのも良い。
ノートに考えを書いてみましょう。
簡単だよ。
たぶん分かった!
子どもたちのノートを見て回ると、予想通り2種類の式が書かれていた。
せーので式を言ってみよう。せーの…
12÷3=4(24人)
12÷4=3(6人)
あれ!?違う式が聞こえてきた。
そうだね。12÷3=4という人と12÷4=3という人がいましたね。
どうして12÷4=3なの?
どっちが正しいのかな?
212÷3=4と考えた理由を全体で解釈する(20分)
選んだ式が正しいと考える理由や選ばなかった式が正しくないと考える理由は何ですか?
ここでは、12÷3=4を先に扱っていった。12÷3=4を考えた子たちは何か言いたそうな表情をしており、これまで主に扱ってきた等分除であるため、誰もがイメージしやすいからである。また、12÷4=3を考えた子は少なく、あまり自信がなさそうに見えた。包含除の方はイメージがしづらいだろう。
12÷3=4の「12」は「全部のあめの数」を表しているでしょ?「3」は「分ける人数」で、「4」は「一人分のあめの数」を表していると思うから、12÷3=4だと思う。
そうだね。言葉の式にするとよく分かるね。僕は問題文をイメージしたよ。
問題文というのはどういうことかな?みんなイメージできるかな?。
私も問題文をイメージしたよ。
12個のあめがあります。3人で分けるには一人何個ずつになりますか?
わり算の逆のかけ算で考えてみても、この問題なら図と合うと思うよ。
本当だね。かけ算で考えるっていいね。
それに、12÷4=3だったら、図が違うと思う。こういう図になるよ(下の写真)。
言われてみればそうかもしれない…。考えが変わってきたかも(12÷4=3と考えた一部の子たち)。12÷3=4なのかな…。
312÷4=3について全体で解釈し、考えを比較する(15分)
さっきみんなが説明してくれたように、12÷3=4の式と図が合っているという意見は納得できる人が多いみたいですね。先生もなるほど!と思いました。でも、まだモヤモヤしている人もいるようです。
実は、先生は12÷4=3の式をイメージして図をかいたんです。
ここで12÷4=3の子を指名して考えを述べさせようと考えた。しかし、自学級では、12÷4=3をイメージした子たちがなかなか自信をもてずにいたため、12÷4=3の式をイメージした子たちの背中を押そうと考えて上記のようにゆさぶる発問を行った。
え!?うそでしょ?
やっぱり!ぼくはこう考えたよ。
あめが12個あります。4個ずつ分けます。何人で分けられますか?
あ〜なるほど!その問題文ならたしかに図とも合っているね。
どっちの式も正しいってことか。
どっちの式も正しいということが分かったね。2つの問題文を見比べてみよう。同じ部分と違う部分は何だろう?
どっちもあめが12個あるというのは同じだね。
違うところは2つあるよ。
違うところは2つあると言っている人がいますが、2つ見付けられますか? それぞれの問題文に線を引きましょう。
分かったよ。△人で分けるか□個ずつ分けるかの違い。
「分け方」が違うってことだよね。
もう一つは最後の一文。一人分が何個かと何人で分けるかという「分からないところ」が違うよ。
そうですね。2つの違うところがあるだけで、どっちの式も図に合っているということが分かりましたね。では、それぞれの式と問題文を図で表してみましょう。
授業のとっておきポイント
「一つの図から2通りの式をイメージすることができる」というのがおもしろいと思い、考えた授業である。前時に、18個のあめを2人で同じ数ずつ分けると1人分はいくつでしょうか?」(18÷2=9)という等分除の場面を図で表すという活動を行った。そのとき、18÷2を意識しているが、「18個のあめを2個ずつ分けると何人に分けられますか?」という包含除の図をかいている人が複数いることが分かった。その思考のずれを問題としたということである。案の定、子どもからは2つの式が出てきた。
今回は包含除の導入として行った。わり算と聞くと等分除をイメージする人が多い。わり算の学習を等分除から導入しているということももちろん関係しているだろう。本時では、図から入ったことで自然と2つの式が登場し、それぞれの式について図を通して解釈していくことで、わり算には2種類のパターンがあることを自然な形で導入することができたのではないだろうか。