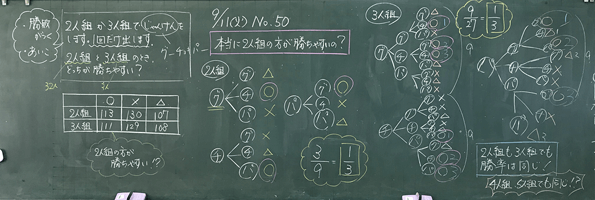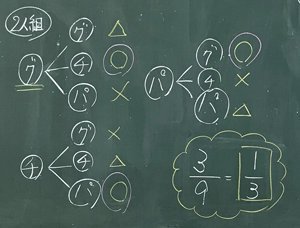- とっておき算数授業
- 算数・数学
本時のねらい
2人組と3人組のじゃんけんでの勝ち負けについて、どちらが1回のじゃんけんで勝ちやすいかを比べる活動を通して、落ちや重なりなく調べる方法(樹形図)についての理解を深める。
板書
板書のとっておきポイント
- (1)問題(2)2人組を調べた結果(3)3人組を調べた結果というように、黒板を3分割して整理した。
授業の流れ
1実際にじゃんけんをした結果を整理し、問いをもつ(15分)
子どもたちが給食の残り物じゃんけんをしているときの2枚の写真を映し出す。1枚目は大人数でじゃんけんをしているときの写真。2枚目は2人組に分かれてじゃんけんをしているときの写真。
給食じゃんけんをしているときの写真です。2枚の様子を比べて気付くことはありますか?
1枚目は大人数でじゃんけんをしているね。なかなか決まらないんだよね。
2枚目は2人だから、割とすぐに決まる。
人数が少ない方がじゃんけんは勝ち負けが決まりやすいと思う。
なるほど。では、たとえば2人組と3人組では、2人組の方が勝ちやすいと言えるかな?
たぶんそうだと思う。
いや、意外と3人組もあまり変わらないとか?
3人組の方が決まりやすいというのは想像できない。
2人組か3人組でじゃんけんをします。1回だけ出すとき、2人組と3人組では、どっちが勝ちやすいかな?
実際にやってみたい。
2人組と3人組でじゃんけんをして結果を調べよう。
2人組と3人組をそれぞれ作り、各自10回ずつじゃんけんをさせた。その結果を表に整理した。ここでは、じゃんけんは「あいこ」も1回分としてカウントすることを確認した。
2人組も3人組もほとんど変わらないね。
でも、ちょっとの差だけど、2人組の方が勝ちやすいという結果になってはいるよね。
えー、誤差なんじゃない?
実際の授業では、小差ではあったが、2人組の方が勝ちやすいという意見が優勢となったため、本当に2人組が勝ちやすいと言えるのか?という問いを設定した。
しかし、実際のじゃんけんの結果次第では、3人組の方に意見が偏るかもしれないし、どっちも変わらないのではないか?という意見に落ち着くかもしれない。その際も、「本当にそうなのか?」と思考に揺さぶりを掛けることで、実際に樹形図を用いて確かめる流れへともっていくことができるだろう。
2樹形図を用いて、2人組と3人組の勝ち方を調べる(20分)
算数を苦手にしている子がこの時点でついてこられなくなってしまう可能性があったため、「2人組」は全体で進めていくことにした。
まずは、2人組について樹形図でじゃんけんの出し方と結果を整理していきましょう。自分がグーを出したとすると、相手の出し方は何通りですか?
グーに対しては、グー・チョキ・パーの3通りだね。
チョキとパーに対しても同じように3通りずつあるよ。
ということは、全部で3×3で9通りってことだね。
そのうち、勝っているのは、グー・チョキ・パーで1つずつだから3通りだね。
つまり、9回中3回勝つから、3/9=1/3の確率で勝つと言えるね。
*確率の考え方は中学校内容であるが、子どもたちは日常的に割合に触れており、9回中3回勝つということを分数で表すことと確率を同じように捉えるのは自然な感覚なのだろうと考え、そのまま扱うこととした。
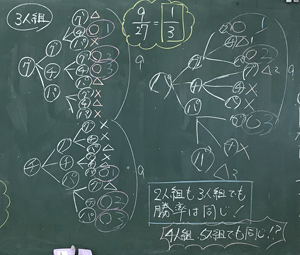
同じようにして、3人組の場合も調べてみましょう。ちなみに、3人組の場合、樹形図は2人組のときとどこが変わるかな?
3人目がいるから、グー・グーの後にグー・チョキ・パーとさらに枝分かれすることになる。
なるほど。では、続きをかいて調べてみましょう。
5分ほど自力思考の時間をとり、その後全体で結果を共有した。
3人組のときも、27回中9回勝つから、9/27=1/3の確率で勝つということだ。
ということは…2人組と3人組は勝率は同じってことだ。
34人組のじゃんけんについて考える(10分)
2人組も3人組も勝ちやすさは変わらないってことが分かりましたね。
人数が多くなっても勝ちやすさは変わらないってこと?
本当にそうかな?人数が多いとあいこばっかで全然勝ち負けが決まらないイメージが強いよ。
*もし、人数が多い場合を考えようとする子どもが出てこない場合は、導入で見せたじゃんけんの様子を再度想起させ、思考に揺さぶりを掛ける。
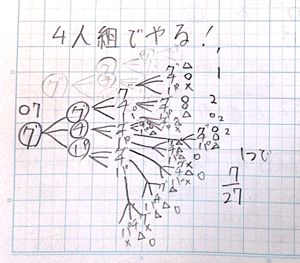
では、4人組のじゃんけんについても樹形図で調べてみましょう。
4人組だと、21/81=7/27だから…2人組や3人組のときよりも確率が低い。
やっぱりいつでも確率が同じわけじゃないんだ。
4人組みたいに多くなっていくと、1発で勝つ確率は低くなるんだね。
もしかして、じゃんけんにグー・チョキ・パーの3つの出し方があるから3人までは同じ確率で、4人以上だと出すものが被ってしまうからあいこの確率が上がるんじゃないかな?
ということは、きっと5人組のときはもっと勝てる確率が下がるってことだね。自学で調べてみよう。
授業のとっておきポイント
今回は、子どもにとっても身近な「じゃんけん」を教材として扱った。誰しもが、人数が多い方が勝ち負けが付きにくいという感覚をもっている(にもかかわらず子どもは大勢でじゃんけんをしがちである)。2人組と3人組では、2人組の方が勝ちやすいと考える子が多い。
そこで、じゃんけんの結果について樹形図を用いて調べてみることで、子どもたちの感覚とのズレが生じる(実際は2人組も3人組も勝ちやすさは同じ)。じゃんけんの勝ちやすさに人数は関係ないのか?という新たな問いを4人組のじゃんけんについて調べることで解決するという流れになっている。このように、問いが連続することで、子どもが主体的に動く授業を目指した。