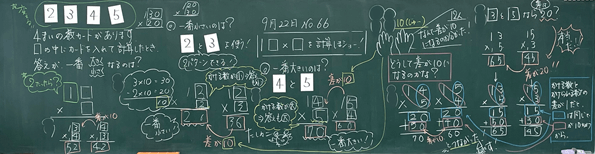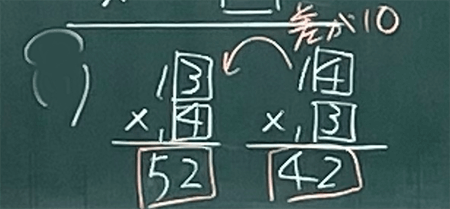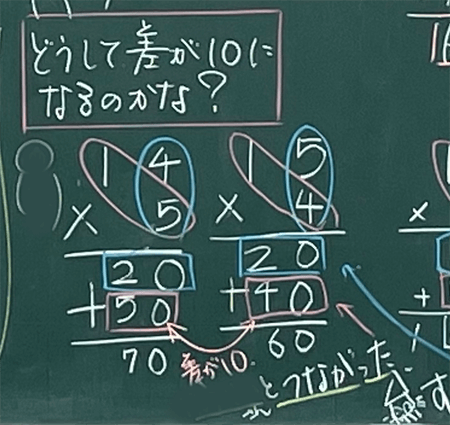- とっておき算数授業
- 算数・数学
本時のねらい
1□×△と1△×□の積の差について、□と△の差の10倍だけ変わる理由を考えることを通して、筆算の仕組みを見直す。
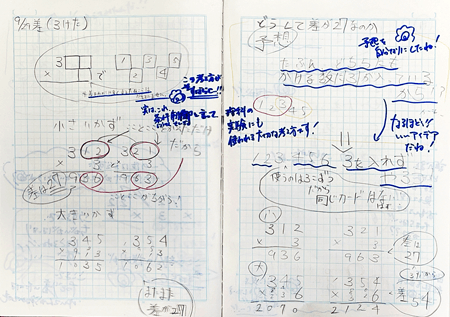
板書
板書のとっておきポイント
- きまり(積の差が10になるという共通点)に気付く段階と、きまりが成り立つ理由について考える(筆算の仕組みを見直す)段階で黒板を大きく二分した。
- 子どもがきまり(積の差が10になるという共通点)に着目できるよう、2種類の差((1)□に入る2枚のカードの差と(2)積の差)に関する子どもの気付きをできる限り板書するようにした。
授業の流れ
1答えが最小・最大になる式を考える(20分)
2、3、4、5の4枚の数カードがあります。1□×□という式の□の中にカードを入れて計算したとき、答えが一番大きく(小さく)なるのはどんなときでしょう。
答えが一番小さくなるようにしたいとき、どのカードを使いたい?
それはもちろん2と3でしょ。
うん。でも2パターンの式ができるよ。
確かに。13×2と12×3ができるね。
どっちが小さいか計算して確かめてみよう。
結果を確認しましょう。
13×2のときの方が小さくなったよ。
私も同じ。13×2の方が10小さい答えだった。
差が10だという板書を残しておく。
次は、一番大きい答えを考えてみよう。
今度は4と5のカードを入れればいいね。
今回も2パターンの式ができるよ。
14×5と15×4では、どっちが大きい答えになるのかな。
14×5の方が大きくなった。かける数が小さいと答えも小さくなるし、かける数が大きいと答えも大きくなるみたいだね。
自力思考中に、隣同士で計算結果を見ながら両手で「10」を作って笑っている子たちがいた。今回はその子たちの表現を全体に広め、きまりへの気付きを促すことにした。
○○さんと△△さんが計算結果を見て、お互いに両手の掌を広げて笑っていたんだけど、2人は何でそんなことをしていたんだと思う?
分かったよ。「10」って言いたいんでしょ?
あ〜!今回も差が10って意味の「10」だね!
どうして今回も差が10になったんだろう?
たまたまじゃないの?
いや、たまたまじゃないよ!これはきまりだよ!だって、13×4と14×3でやってみても、差が10になったもん。
えー!不思議だ…。
2差が10になる理由について考える(15分)
最初のうちは、口頭でのぼんやりとした説明や(かけられる数の十の位)×(かける数の一の位)の部分の説明(“違い”にだけ目を向けている)が続き、なかなか理解が深まらない様子だった。そこで、筆算を2段にして表現していた子がいたため、多くの子がきまりに気づくきっかけとなると思い、指名した。
たぶんだけど、差が10になる理由が分かった気がする。筆算を2段で表す方法も勉強しましたよね。今回も2段で表してみたんだけど…。
あっ!何か分かったかも!1段目の20は同じだけど、2段目の50と40の差が10になっている。
そっか!1段目の20は5×4と4×5で入れ替えても答えは変わらないもんね。だけど、2段目は5×10と4×10で差が10になるんだ。
○○さんが言いたいことが分かったかな?隣の人と確認してみよう。
○○さんは、一の位同士のかけ算は入れ替えても答えは変わらないけど、十の位と一の位のかけ算は片方は5で、もう片方は4だから、それに10をかけるから差が10になるって言いたいんだと思う。
そうそう。なるほどだね。
3見付けたきまりを発展させる(10分)
もしかして、これってカードの差が1だから何じゃない?
じゃあ、カードの差が1じゃないような、たとえば3と5だったら差が20とかになるのかな?
□□さんの予想をみんなで確かめてみよう。
13×5と15×3だから…あっ!本当に差が20になったよ。
すごい!不思議だ…。
さっきみたいに2段の筆算で表してみたら理由が分かったよ。
さっきと同じで、1段目はやっぱり同じ答えになって、2段目の計算の答えの差が正体だよ!
おもしろいね〜!
この問題を自分なりに発展させるとしたら、どんなふうに問題を変えてみたい?
最初の4枚のカードを別な数字に変えてみたい!
もともとの式は十の位が「1」だけど、他の数字、たとえば「2」だったらどうなるのか試してみたい!
自主学習で続きを調べてみるといいね。
下はその後の実際の自主学習ノート。
授業のとっておきポイント
この教材の良さは大きく2つあると考えている。
(1)□を用いたり、用いる数カードを固定したりすることで思考を絞り、全体の学びを方向付けすることができる(思考が拡散しない)。
本時のねらいは、「筆算の仕組みを見直すこと」である。問題に制限を設けることで、仕組みに着目できるようにしているのである。答えが一番小さくなる場合と一番大きくなる場合の2通りを扱うことで、きまり(どちらも積の差が10になるという共通点)が見える。そして、その理由を考える中で筆算の仕組みを見直すことができる。形式的になりがちな筆算の学習だが、こういった学習を挟むことで、仕組みを振り返る機会とすることができる。
(2)□に入れる数を変えたり、固定した部分の数値を変えたりすることができ、発展性がある。
授業を考える際には、授業後の子どもの学びを想定することも大切である。発展性のある教材を扱うことは、「だったら〜のときはどうかな?」「もしかして〜じゃないかな?」などというように、授業で学んだことの先を見る子どもを育てていくことにつながる。子どもから動き出せるようになるまでは、授業の中でくり返し、「この問題を自分なりに発展させるとしたら、どんなふうに問題を変えてみたい?」というように問い掛けるようにしている。次第に、「だったら…」と動き出す子が現れるようになる。そのときは価値付け、また全体に広めていく。このくり返しを大切にしている。
【参考文献】
田中博史監修、夏坂哲志著『板書で見る全単元・全時間の授業のすべて 算数 小学校3年上』(東洋館出版社、2020年)