- �Ƃ��Ă����Z������
- �Z���E���w
�{���̂˂炢
�@�уO���t��~�O���t�̓����𑨂��A�u���Ƃɂ���ʂ͉����v�ɒ��ڂ��āA�S�̂ɑ��邻�ꂼ��̕����̊��������߁A�уO���t��~�O���t�ɕ\���B
��
���̂Ƃ��Ă����|�C���g
- �b�����̃��C���ɂƂȂ�уO���t�����̒��S�ɐ����A�����̌v�Z�Ƃ̂Ȃ��肪������悤�ɉ�������B
���Ƃ̗���
1���s���̃O���t����₢�������i15���j
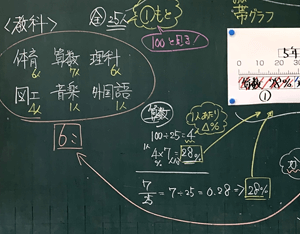
�@���炩���ߎq�ǂ������ɃA���P�[�g���Ƃ��Ă����A���̌��ʂ����Ƃɗp���邱�ƂƂ����B�������̂́u�D���ȋ��ȁv�ŁA�[���������̂�6���ځB�w���̐l����25�l�ł������B
�݂�ȂɃA���P�[�g���Ƃ����u�D���ȋ��ȁv�̌��ʂ\���܂��B
�Z����1�ʂ��ˁB
6��ނ����[������Ȃ������ˁB
���̌��ʂ��O���t�ɕ\���Ă݂܂��傤�B����́A���̃O���t�p�����g���܂��B
�����H25�l�������Ȃ��̂ɁA�ǂ����Ėڐ��肪100�܂ł���́H
�{�����B�܂����������Ƃ������B����[���������̂�6��ނȂ̂ɁA�O���t�ɏ������߂�g��5���������Ȃ���B
���������B���������Ȃ����炩�킢�����B
�Ȃ�قǁB���������Ƃ�����Ƃ������Ƃł��ˁB
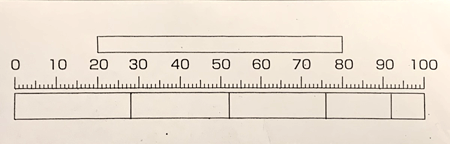
�@��̎ʐ^�̂悤�ȃO���t�p�������ƁA�q�ǂ������͂��܂��܂ȍ��芴�����ɂ���B����o�Ă����̂́A�ȉ���2�_�ł���B
�i1�j�ő��25�[�����Ȃ��̂ɁA�ڐ���̍ő�l��100�ł��邱�ƁB
�i2�j�[���������̂�6���ڂȂ̂ɁA�O���t�ɓ����Ă����ڂɂ��܂Ƃ܂��5���������Ȃ����ƁB
�@���ꂼ��̘b��ɂ��đS�̂ŏ��Ɉ����Ă����B�܂��́i1�j�ɂ��ĉ������邱�Ƃɂ����B
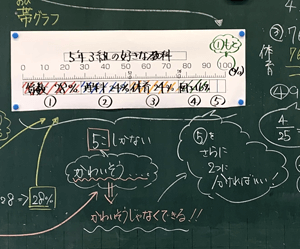
2�[����������p���ĕ\���i15���j
�ł́A�܂��u�ڐ���̐������������v�Ƃ������Ƃɂ��Ăǂ������Ă���̂��A�݂�Ȃōl���Ă݂܂��傤�B�Z�Z�������Ă����u�ڐ���̐������������v�Ƃ����̂͂ǂ��������Ƃ��ȁH
�N���X�̐l����25�l������[���S����25�[�ł���ˁB����Ȃ̂ɁA�O���t�̖ڐ��肪100�܂ł���̂͂��������Ǝv���B
���������B30���炢�܂ł���Ώ\���B
���������B�u100�v�ƌ����A�S�����ł���H�l���������ŕ\��������Ȃ����ȁB
�������B�S�̂̐l���ł���25��100�ƌ��������ŕ\���������Ă��Ƃ��ˁB
����͑S�̂̐��ł���25�����Ƃɂ���ʂƌ���������Ă��Ƃ��B
�����ōl����Ƃ��������A�ƂĂ������ł��ˁB�ł́A��ԑ��������Z���ɂ��āA�S���ōl���Ă݂܂��傤�B
100��25��4�A4�~7��28�i���j�ƍl���܂����B
���́u4�v���ĉ���\���Ă���̂��ȁH
���`��A�����낤�ȁc�B
100����25�l�Ŋ����Ă��邩��c1�l�����艽���������߂Ă����Ȃ����ȁH
�ڂ��͕ʂ̍l������������B25�l��7�l����ƍl���āA�����ŕ\���܂����B7�^25��7��25��0.28�i28���j
�����I���ꂪ�O���t�̈�ԍ��̕������ˁB�҂�����28������B
����ő��̋��Ȃ̊��������߂�ꂻ���ł��ˁB
�@���Ԃ��Ƃ�A���̋��Ȃ̊������v�Z�ŋ��߂����Ă������B
3���߂�������p���ăO���t�������������i15���j
����H�҂��āA�搶�B���������A������̖�肪�������Ă��Ȃ���B
������̖��Ƃ͉��ł��������H
6���ڂ���̂�5���������Ȃ����B
���������B������������Ȃ��ƁA���������߂Ă��O���t�ɕ\���Ȃ��ˁB
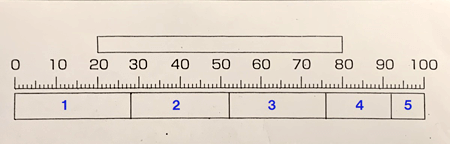
���Ԃɓ���Ă��炦�Ȃ��Ƃ��킢��������B
���킢��������Ȃ��ł����I
�����ł����B�D�̏ꏊ�������2�ɕ����������I
���[�I�Ȃ�قǁI
���̕��@�������I�]�v���킢�����Ȉ�������������Ȃ����ǁc���y�ƊO������u���̑��v�ɂ��������B
���[�I���̑��ˁI�������ɂ��̎肪�������ˁB���킢���������ǁA�l�������Ȃ������̑��Ƃ��ĂЂƂ܂Ƃ߂ɂ�����̂������Ȃ����@����ˁB
�ł́A���y�ƊO����́u���̑��v�Ƃ��Ă܂Ƃ߂邱�ƂƂ��āA�уO���t�����������܂��傤�B
�@�Ō�ɉ~�O���t����A���������w�������B�l�ʼn~�O���t���쐬���鎞�Ԃ��Ƃ��Ď��Ƃ��I�����B
���Ƃ̂Ƃ��Ă����|�C���g
�@������A���s���̃O���t�p������邱�ƂŎq�ǂ��̍��芴�������o�����B�����āA���̍��芴��S�̂ŋ��L���A�������Ă����W�J�Ƃ����B
�S�̂̐���100�̃O���t����邱�ƂŁA�O�P���Ŋw�K���������i�S�����j��z�N������B�S�̂̐���25�����Ȃ����̂�100�ŕ\���A�܂�u25��100�ƌ���v�Ƃ����u���Ƃɂ���ʁv�̌����������o���B���̎��Ƃōŏ��ɑ�ɂ��������Ƃł���B����͊w���̐l����25�l�Ƃ��傤�Ǘǂ������������A�w���̐l���������Ȃ����̏ꍇ�́A�Ӑ}�I�ȃf�[�^����Ă��ǂ��B�����������v�Z�������Ă���ƁA�v�Z�Ɏ��Ԃ��������Ă��܂�����A���ė����Ȃ��Ȃ��Ă��܂����肷��q���o�Ă��܂��A�����ƑуO���t�E�~�O���t�Ƃ̊W�ɖڂ������Ȃ��Ȃ��Ă��܂��\��������B
�@�܂��A����̂悤�ȏꍇ�́A���Ƃɂ���ʂ��ς��Ȃ����ߊ����𑫂������������ł���B�������A���Ƃɂ���ʂ��قȂ�ꍇ�͊����𑫂�����������肷�邱�Ƃ͂ł��Ȃ��B���̓_�ɂ����ӂ��Ďw���������B