大野桂の算数熱中授業づくり
わかった！　楽しい！　そんな子どもの声が教室に響く算数の授業をつくりたい。 発問、板書から子どもの意見の取り上げ方まで、学級全員を熱中させる工夫やアイデアを大公開!!
大野桂の算数熱中授業づくり（4）
倍で比べる？　差で比べる？（5年「割合」）
【問題提示】と【説明の場】の工夫
筑波大学附属小学校教諭大野　桂
2013/9/25 掲載

熱中授業づくりのポイント

  1. 誤概念を含む問題提示
  2. 「他の場面に置き換える」という方法で説明する場を設ける
  3. 「共通性を探る」ことで割合の概念を自然に獲得させる

1　誤概念を含む問題提示

　5年「割合」の導入教材です。正しい概念に基づく「倍による比較」と、誤概念に基づく「差による比較」を提示し、2つを対峙させてその妥当性を吟味する中で、割合の概念を獲得させていきます。

　下のチョコ棒はMサイズです。
Mサイズ　全体30cm、チョコ20cm

　いま、全体の長さが45cmである、Lサイズのチョコ棒をつくろうとしています。アとイどちらの長さだけチョコをぬればよいでしょうか。
Lサイズ（ア）　全体45cm、チョコ30cm

Lサイズ（イ）　全体45cm、チョコ35cm

　アは「倍による比較」であり、イは全体が15cm伸びたからチョコも15cm伸びるという「差による比較」です。

●倍による比較

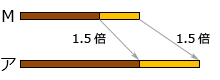倍による比較図　全　体：45÷30＝1.5（倍）

　チョコ：30÷20＝1.5（倍）

●差による比較

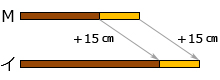差による比較図　全　体：45−30＝15（cm）

　チョコ：35−20＝15（cm）

2　「他の場面に置き換える」という方法で説明する場を設ける

　下のように、「他の場面に置き換える」という方法で、それぞれの比較の仕方が適切か否かを説明する場を設けます。学習内容の理解とともに、このような問題解決力を子どもに身に付けさせることも意識したいものです。

●差による比較に関する説明

Ｃ　Mを60cm伸ばして90cmにする。チョコも60cm伸ばすとすると、チョコが多すぎて明らかにバランスがおかしい。

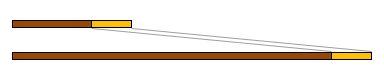
差による比較図（90cm）

Ｃ　Mを20cm短くしたら、チョコも20cm短くすることになる。そうするとチョコがなくなってしまうので、同じようにチョコをぬっていると言えない。

差による比較図（10cm）

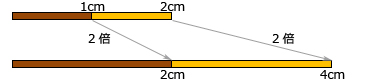
●倍による比較に関する説明

Ｃ　全体が2cm、チョコが半分の1cmぬられているとしたら、全体を4cmに伸ばすと、チョコは全体の半分の2cmぬられることになる。

倍による比較図（2倍）

Ｃ　全体の長さを2倍伸ばしたら、チョコの長さも2倍伸ばすということ。
Ｃ　伸ばす前と後でバランスが変わらない。

3　「共通性を探る」ことで割合の概念を獲得させる

　「倍による比較」が妥当であると判断されたら、次は、倍の方法で様々なサイズのチョコ棒をつくり、その全体の長さとチョコの長さの共通性を探らせます。
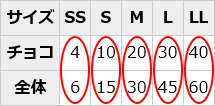
さまざまなチョコ棒

Ｔ　どのサイズも同じようにチョコがぬられているとはどういうこと？（チョコと全体の数の対応に着目させるため○で囲む）

C　全体の長さがチョコの長さの1.5倍になっているということ。
全体÷チョコ＝1.5

C　チョコの長さが全体の長さの2/3倍になっているということ。
チョコ÷全体＝2/3

Ｔ　そのような、「一方を1とみたときに、もう一方がいくつに当たるか」、つまり「何倍に当たるかの数値」を“割合”といいます。

　この授業では、「サイズが変わっても変わらないものは何か」を考えさせる活動を通して、割合の概念をより自然に獲得させようとしました。
　このような、「共通性を探る」という方法も、子どもに身に付けさせたい問題解決力の重要な1つです。

大野　桂（おおの　けい）

1976年東京都生まれ。東京学芸大学卒業。私立高等学校、東京都公立中学校、東京学芸大学附属世田谷小学校を経て、2010年より筑波大学附属小学校教諭。
日本数学教育学会編集部幹事、教育出版教科書『小学算数』編集委員、全国算数授業研究会常任理事、使える授業ベーシック研究会常任理事、『算数授業研究』編集委員。
筑波大学附属小学校算数部ブログ

（構成：矢口）
コメントの受付は終了しました。