- 協働的な学び
- 算数・数学
「個別最適な学び」と「協働的な学び」を行う際、評価について考えることは避けては通れない問題です。
評価とひと言でいっても、様々な考え方があります。ABCといった評定をつけるという意味もあれば、教師が授業改善や子どもへの指導の仕方を再考するための評価という意味もあります。
今回は、意図的目標評価と無意図的目標評価という考え方を基に、「個別最適な学び」における評価について述べていきます。
各教科が育てるべき力とは何か
教科教育における評価を考える際、最初に考えるべきことは、「その教科で育てるべき力は何か」ということです。算数であれば、小学校学習指導要領の算数科の目標が、算数で育てるべき力ということになります。とはいえ、教科目標をすべて頭に入れながら日々の授業で評価を行っていくのは、なかなか難しいことです。そこで、教科目標に書かれていることを基に、教科特性に応じた「その教科で育てるべき力」について、端的な言葉でまとめることが必要だと考えています。
小学校学習指導要領の算数科の目標の(3)に関する解説において、「算数は系統的な内容によって構成されており、児童が常に創造的かつ発展的に算数の内容に関わりをもち学び進むことが期待されている」(文部科学省、2017)と示されている通り、算数というのは、内容の系統性がとても強く、既習事項やまわりの人たちの考え方を使えば、新しい知識を子ども自身で創り出すことができる教科なのです。よって、算数で育てるべき力については、「既習事項や様々な考え方を使って、新しい知識を創造する力」(この「新しい知識」とは、言葉や記号の意味、公式、計算の仕方等の技能のみに限らず、問題解決のための着眼点や思考方法も含む)とまとめることができるのではないでしょうか。
「個別最適な学び」における評価について
加藤(1982)は、学習に先立って定められる学習の目標を意図的目標、最初に意図しなかった目標を無意図的目標と述べ、実際の学習活動では教師が定めた目標とは別の目標を目指して思考を進める子どもがいることを指摘しています。「個別最適な学び」を考える際、無意図的目標を用いた評価(以降、無意図的目標評価)を無視することはできなくなります。
では、無意図的目標は「何でもよい」のでしょうか。私は、価値ある無意図的目標と、そうでない無意図的目標があると考えます。教科教育で「個別最適な学び」を考えるのであれば、やはり教科特性に応じた力を身につけているかどうかという視点が評価として大切になると思います。算数でいえば、「既習事項や様々な考え方を使って、新しい知識を創造する力」を身につけているかどうかが、無意図的目標評価においても大切な評価規準・基準になるのです。
「個別最適な学び」といっても、「指導の個別化」と「学習の個性化」では、学習のあり方が異なります。よって、それぞれの学習における評価について考える必要があります。加藤(1982)は、意図的目標を用いた評価(以降、意図的目標評価)は「指導の個別化」に関わる評価活動、無意図的目標評価は「指導の個別化」と「学習の個性化」に関わる評価活動と述べています。無意図的目標評価は、「指導の個別化」に関わることもありますが、特に「学習の個性化」の場面において重要になると考えられます。子どもが自ら学習を進めるような姿こそ、「個別最適な学び」において評価すべきことなのです。
①「指導の個別化」における評価
「指導の個別化」とは、一人ひとりの学力や特性に合わせて、子どもが学習内容や学び方を選択し、基礎・基本となる知識や学び方を身につける学びといえるでしょう。少し乱暴ないい方になりますが、教科書の内容を、一人ひとりの特性や学習進度に合わせて身につけさせていくことと考えるとわかりやすいでしょう。
意図的目標評価は、「指導の個別化」において用いるのに適した評価ですから、「指導の個別化」における評価については、意図的目標評価について考えるとよいでしょう。ただし、「○○という知識を獲得すること」という目標を定めることが意図的目標ではありません。意図的目標は、「行動目標」として記述することになります(加藤、1982)。子どもを主語にして、「~考える」とか「~関連づける」のような動詞で記述するということです。この子どもの「行動目標」を各時間で言語化しておくことが、意図的目標になるということです。
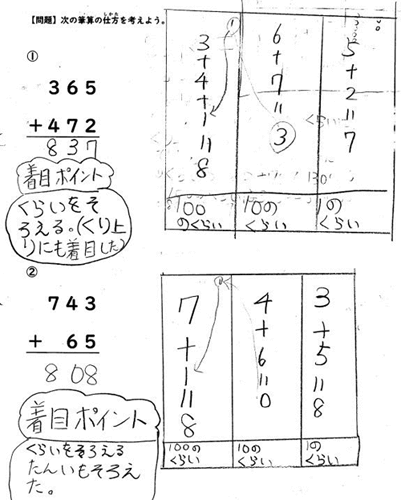
例えば、3年「大きい数のたし算・ひき算の筆算」の単元の2時間目において、次のような問題を扱う学習をしました。
次の筆算の仕方を考えよう。
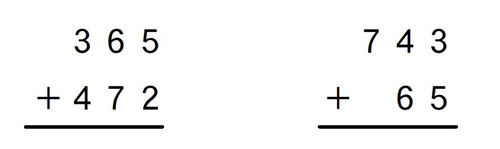
この問題を考える学習は、個別学習で行いました。下のノートは、その際に、ある子どもが書いたものです。
位に着目するとともに、「位をそろえることは、何をしていることなのか」ということについても書かれています。それが、左下の「着目ポイント くらいをそろえる たんいもそろえる」という言葉で表されています。
ただ答えが求められるだけでは、算数で育てるべき力である「既習事項や様々な考え方を使って、新しい知識を創造する力」とはいえないでしょう。この場合であれば、既習であるたし算との関連を想起して、「今までやったたし算と共通することは何か?」についても考えてほしいところです。たし算には「同じ単位どうしでないとたすことができない」という原理があります。そのたし算の原理を筆算でも当てはめながら、「位をそろえるということは、単位をそろえていることだ」ということまで考えて、意図的目標として定めたのです。最終的には、「既習であるたし算の原理と3位数+3位数の筆算の仕方の共通点を考え、答えを求めることができる」としました。
もちろん、子どもだけで、既習のたし算と結びつけるのは難しいことです。ですから、個別学習をしている子どもに対して、「たし算って、同じ単位どうししかたせなかったの覚えている? だったら、位をそろえて計算するってみんなはいってるけど、今までたし算でやっていた、単位をそろえて計算するってことを使って、位をそろえることが何をしていることか考えられるかな?」といった声かけをするのです。子どもだけで価値ある発見ができないと判断したら、教師の声かけは必要です。だからこそ、意図的目標を定めることで、意図的目標に到達するのが難しいようであれば、学習中でも指導の改善を試みることが可能となるのです。
②「学習の個性化」における評価
「学習の個性化」とは、一人ひとりの興味・関心や必要性に合わせて、自ら学習を発展させ、探究していく学びといえるでしょう。こちらも、少し乱暴ないい方をすれば、一人ひとりの興味・関心に合わせて、教科書の内容から飛び出し、探究していく学習と考えるとわかりやすいかもしれません。
「学習の個性化」においても、あらかじめ教師が想定していた範囲で、子どもが学習を発展させる場合があります。その場合は、意図的目標評価が可能となります。しかし、「学習の個性化」においては、無意図的目標評価が不可欠です。なぜなら、「学習の個性化」において、子どもは事前の想定を超えた活動をする場合があるからです。
例えば、3年「あまりのあるわり算」の単元において、次のような問題を扱う学習をしました。
ミニカーが7台あります。
3人で仲良く分けると、1人分は何台になって、何台あまるでしょうか。
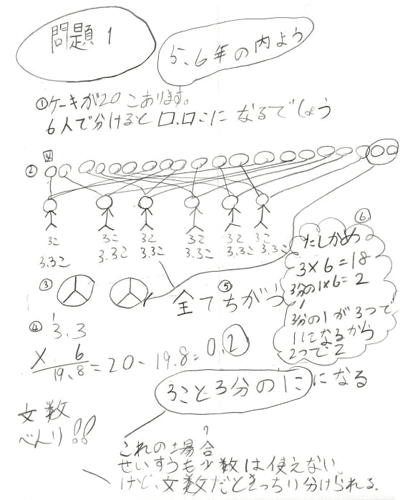
この問題を解決した後、多くの子どもは、あまりのある等分除のわり算の問題を作問していました。その中で、「ケーキが20こあります。6人で分けると1人分は□こになりますか」という問題をつくった子どもがいました。最初、「1人分は3こで、あまりが2こ」という答えを出していましたが、「でも、ケーキがあまったら、そのままにしないよな」と日常場面を想起して、あまりの2個のケーキを3人でさらに分けようと考えました。下の写真が実際のノートです。
まず、近くにいた小数を知っている友だちからアイデアを聞いて、「3.3こ」という答えを出してました。しかし、3.3×6というたしかめ算をやっても20にならないことから、小数では答えが出ないことに気づきました。そこで、分数を使って、「3こと3分の1こ」という答えを導き出していました。分数を使ってたしかめ算をやってみると、ちゃんと答えが20になることも発見し、分数の便利さを感じていました。もちろん、分数のかけ算とわり算は知りませんが、分数の意味に立ち返れば考えることができたのです。左下に書いてある「文数(分数)べんり!!」という言葉は、商分数のよさの1つでもある「分数であれば、どんなわり算でも答えば出せる」ということを実感している言葉でしょう。
これはわり進み、小数の乗除、商分数、分数の乗除といった4・5・6年生の学習内容です。しかし、子どもは先行知識をもっている友だちに知識を教えてもらったり、既習事項と結びつけたりしながら、3年生で学習しない内容にも触れていったのです。まさに、無意図的目標評価が必要な場面です。
この姿を見て「これは3年生ではできなからやらなくていいよ」とか、「小数や分数の計算はまだ学校では習っていないから使わないでね」と言ったらどうなるでしょうか。きっと、子どもの算数への探究心はしぼんでしまうでしょう。もっと肯定的に、「3年生の学習を飛び越えて、さらに先の学習を自分で考えることができたね!」と評価をしてあげたいものです。
【参考文献】
・文部科学省(2017)『小学校学習指導要領解説 算数編』(日本文教出版)p.21、28
・加藤幸次(1982)『個別化教育入門』(教育開発研所)p.147、150、155